Understanding Assembly Indices
Calculating the Assembly Index of a molecule is an NP-Hard problem. We've developed a hierarchy of algorthmic approaches to this calculation. Use the descriptions below to understand the outputs from Molecular-Assembly.com.
Molecular Assembly Indices
Molecular Assembly indices are a fundamental quantity in Assembly Theory because they measure
the amount of information required to make a molecule. The Molecular Assembly Index (MA) of a
molecule is defined as the fewest number of steps required to make the molecular graph
by recursively using previously made structures. Let's unpack that statement a bit.
First let's get a feel for this process. Instead of thinking
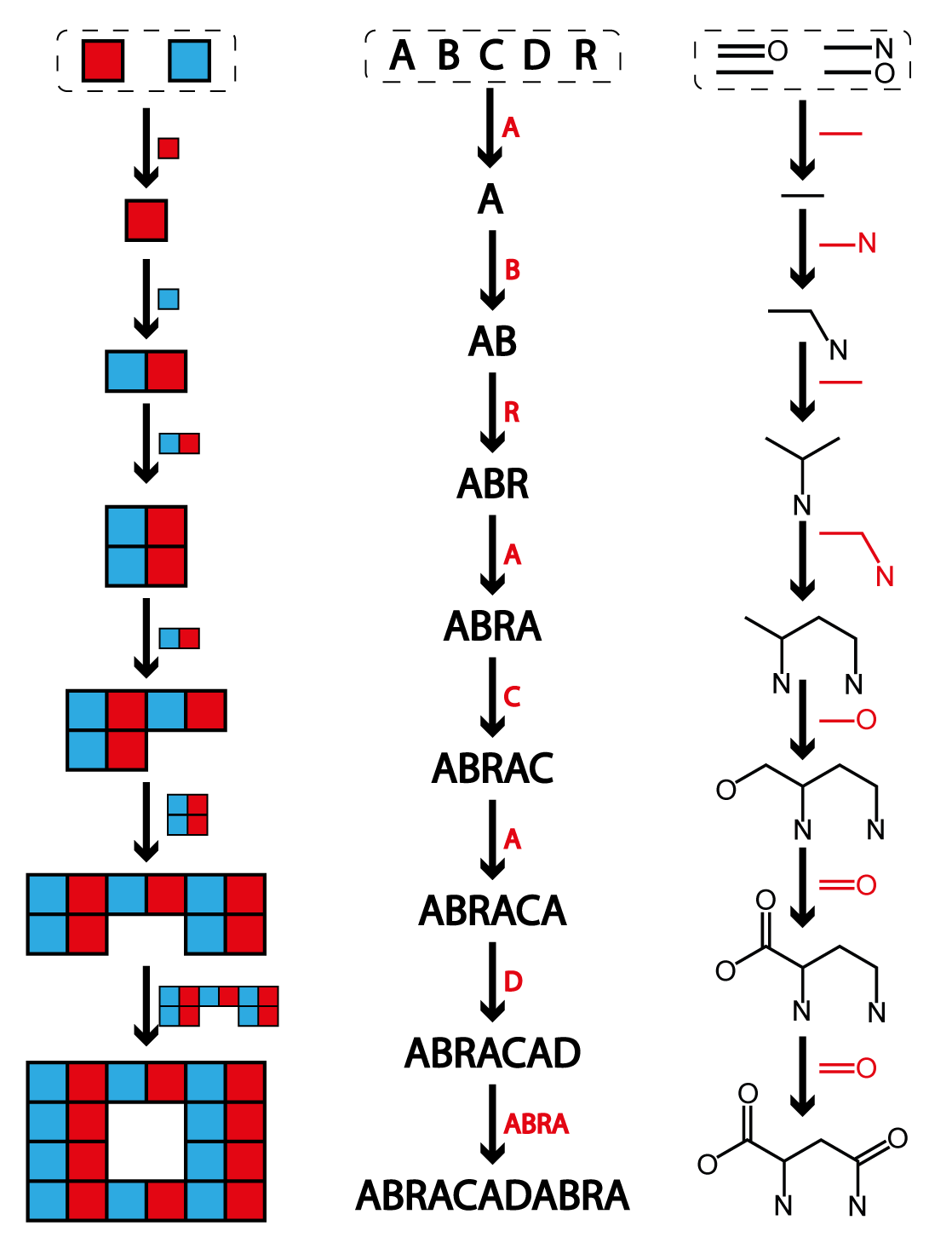
about molecules, let's consider the Assembly Index of a word, like "ABRACADABRA". This example
is
worked out in the image on this page. The word contains nine letters in total, but is built of
four unique letters ("A", "B", "C", "R"). We'll refer to the unique letters in the word as the
"basic building blocks." To start the assembly process we can take a basic building block, in
this case let's start with "A" which we can join with another
building block, "B", to make "AB", that's one step. We can repeat this process a couple times
to make "ABRA", and then a few steps later we will have made "ABRACAD". So far the number of
steps we have taken is six, which is the length of the word we've made so far. To finish the word
we need to add four more letters, but we've previously made the remaining piece we need ("ABRA"),
so we can add all of those in one step, resulting in an Assembly Index of 7. That last step,
where we reused "ABRA", is what we mean when we say "recursively using previously made
structures." We could have taken a longer path to make the final word, for example by reusing
"AB" but adding "R" and "A" at the end in seperate steps. That would have taken a total of 9
steps. When we say the Assembly index is the "fewest number of steps" what we mean is that
there is no way to make the final target using fewer steps - although there might be pathways
that require the same number of steps (for example you can build ABRACADABRA from right to left
instead of left to right in the same number of steps).
We when talk about the Molecular Assembly Index (MA) of a molecule we are talking about the
steps required to make its graph structure, not the molecule itself. That means that we are not
concerned with whether or not the operations we perform in this process could be physically
done in a lab or a natural setting. Therefore some of the joining operations could seem
counterintuitive to chemists or folks who make real molecules for a living. The number of steps
required to make the graph will never be less than the number of individual mechanistic steps
required to make the actual molecule. This is why we emphasize that we are calculating the fewest
number of steps to make the molecular graph, not the molecule. When we compute the MA of a
molecule we ignore the Hydrogen atoms. This is done primarily for computational simplicity
because it significantly reduces the number of atoms in a molecule and has an insignificant
effect on the structure of the compounds. Finally when we consider the basic building blocks of
a molecule, we use the unique bonds in the molecule, not the atoms, as the components. That
means that joining operations are defined by super imposing two (or more) atoms in different
bonds.
Computing the MA of a compound is an NP-Hard problem,
meaning that the comptuational time required to find the answer increases significantly with the size of
the molecule. This is one reason we have decided to have Molecular-Assembly.com look-up precomputed MA values for
molecules rather than compute them de-novo. In order to understand the data that this website
provides it is important to understand the different algorithms we have developed to calculate
MA. We detail the those algorithms below.
Split Branch MA
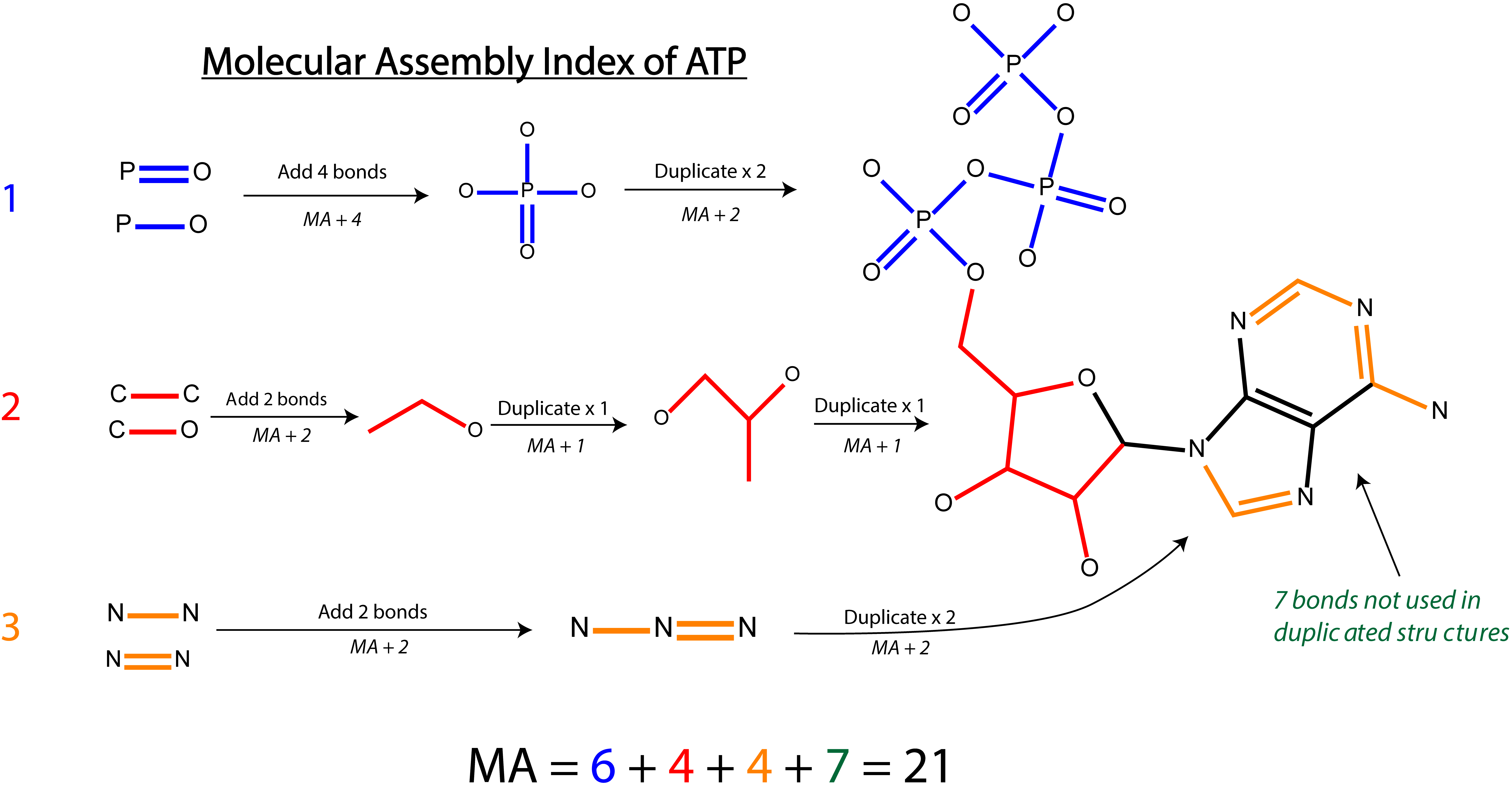
In our 2021 paper entitled Identifying molecules as biosignatures with assembly theory and mass spectrometry we used an algorithm known as a the Split Branch algorithm, which provides an upper bound on the MA of a compound. This means that the MA of the compound is no higher than the value provided by this algorithm. This algorithm was chosen because the algorithm is both simpler and often faster than an exact calculation of the MA. The split branch algorithm computes the MA by first identiying large substructures with little overlap in the target graph, and then computes the MA of those structures independently. This means that if the target is partitioned into two different structures, some motifs that appear in both might be over-counted, resulting in an MA that is higher than the fewest number of steps required to construct the graph. This over-counting will not affect all molecules equally, it will depend on the structure of the molecule itself. We have provided an example of how this algorithm computes the MA of ATP in the figure below. A detailed description of this algorithm can be found in that paper and the associated supplement.